#shc20: Reverence & Revelry

I'm exploring reverence and revelry for the upcoming Southern Humanities Conference to be held in Baton Rouge, LA, this Jan 30 to Feb 01. I will be using Edgar Morin's concept of dialogic to make sense of the engagement and interactions of the two modes of human behavior, especially as these interactions relate to the Southern Humanities community itself. Let's start with some definitions.

The online Oxford English Dictionary defines revelry as "the action or an act of revelling; boisterous mirth or merrymaking; (also in plural) lively entertainments; wild or noisy festivities, esp. those involving drinking." The OED says that the word developed within English itself as a variation of the word revel, a French word that entered English with the Anglo-Normans and means "noisy merriment". The English reworked the term to better manage it into something like "an entertainment or festivity", and eventually institutionalized revelries as a "department of the British Royal Household headed by the Master of the Revels". The OED connects revelry to the term reverie, which has senses both of "wild and uncontrolled behavior" and the more contemplative "being lost in thought or daydreaming."

According to Google's Ngram Viewer, use of the term revelry in English writing peaked in 1850 (.0001497566% of all words used) and suffered a steady decline until 1987 (.0000334220%) at which time it started to recover slightly in usage among writers of English.

1850 saw the publication of Dickens' David Copperfield and Nathaniel Hawthorne's The Scarlett Letter, the Brownings's Sonnets from the Portuguese and Christmas-Eve and Easter-Day, Tennyson's In Memoriam A. H. H., and Wordsworth's The Prelude, and Soren Kierkegaard's Practice in Christianity.

Use of the word reverence peaked earlier in 1823:


But as you can see, it has declined steadily ever since, hitting its low water mark in 1988 and pretty much staying there. To my eye, the usage trends are similar: both peaking in the first half of the Nineteenth century and steadily declining to the present.

If we compare the frequency of usage of the two terms, we see that revelry was never as popular among English writers as was reverence:


I'm not quite sure what to make of this data. It is factual, but I don't know if it means much. I would have been more satisfied if the use of reverence had bottomed during the Romantic era of the early Nineteenth century and picked up during the ensuing Victorian Age and if the use of revelry had trended the reverse, as that would fit nicely my view of the Romantics favoring revelry and the Victorians favoring reverence, but this data does not fit that pattern.

Of course, neither word seems to have ever been prominent in English writing. Their rates of occurrence in 1835, a midpoint of their respective popularities, show that reverence, which was used 24 times as often as revelry, still occurred only .0024% of the time in English. Revelry occurred .0001% of the time. This seems like very small rates of occurrence, but how does it compare to other English words, especially more popular words such as the (the most frequently used English word) and this (the second most frequently used noun)? Google's NGram plots it rates for us:


The word the occurs at a rate of about 5-6% in English texts and this at about .3-.4%. In other words, the occurs 5 or 6 times in every 100 English words of text, and this occurs a little less than once in every 200 words. This is a lot, especially compared to reverence and revelry, but we can see that the frequency of occurrence for all four words declines from 1800 to 2000, which suggests to me that they are all swimming in a larger pool of words. Indeed, science writer Richard Alleyne reports in The Telegraph that the "English language has doubled in the last century." He adds that researchers at Harvard and Google report that "the language has grown by more than 70 per cent since 1950." As the number of available English words and English writers grows, then the frequency of occurrence for any single word -- even a popular word such as the -- decreases.

Still, the decline for both reverence and revelry is much steeper than for the and this. Reverence and revelry appear to be losing their purchase on the minds of writers of English. Why? I can guess that the explosion of new knowledge in the physical and social sciences and in technology (think of computing alone) has given us much more to discuss and diverted our attention away from the old human concerns with reverence and revelry. I associate reverence with God, and so I charted the rate of usage for God (with a capital G) and found a decline in usage similar to that of reverence and revelry:


As you can see, God bottomed out in English letters about 1940 and has not recovered much since. I strongly suspect that God herself is quite well, but English writers are distracted these days with quantum physics, quantum computing, relativity, artificial intelligence, the Internet, gene splicing, global warming, and the cults of personality -- among a google other topics associated with the rise of science and technology and six billion new humans. Really, there's just too much to think about these days, and none of us -- certainly not I -- are bright enough to consider it all.

At a first casual hearing, then, both reverence and revelry sound a bit quaint, as if I am in a medieval chancery court listening to its slow, arcane deliberations about the estates of lunatics and the disposition of foundlings while clarions sound through the cold, open windows. But these are the terms, the parameters, of our conversation, and so I'm wondering what to make of them. That's another post, I think.

RhizoRhetoric: Writing as a Complex System

I've been reading about complexity science and thinking — I prefer here the active form thinking over the static form thought, verb over noun, doing over being — and I want to write a few posts about writing as a complex adaptive system. I will shamelessly pilfer from some of the works that I've been reading to see if I can make some connections between the ancient art of rhetoric and the modern science of complexity. I start with Joss Colchester's short (57 pages) introduction into complexity: Complexity Theory (2016), which is accessible to most anyone interested in the topic.

For Colchester, complex systems are subsets of systems in general. He defines a system as "a group of parts called elements and relations between these parts through which they can function together and form a whole" (5). Colchester then adds complexity to the idea of systems, presumably to distinguish complex systems from other types of systems, presumably complicated or even simple systems, though he is not clear about this. I find it useful, then, to use Snowden's categories of the simple, complicated, complex, and chaotic domains to understand the distinction that Colchester is trying to make with complex systems.

As do many writers dealing with complexity, Colchester begins by noting that "there is no formal definition for it" (5), and then like the others, he lists some characteristics of complexity, noting that complexity can be treated as a parameter, or a measurement of something:

• Complexity is a measurement of the number of elements in a system, with a rule of thumb that the more elements a system has, then the more complex it is.
• Complexity is a measurement of the number of connections among the elements within a system, with a similar rule of thumb: the more connections, the more complexity.
• Complexity is a measurement of the adaptability of the elements. The more elements can adapt to themselves and to their environment, the more complex they are.
• Finally, "complexity is also a measure of the degree of diversity between elements within a system" (6). The more diverse the elements, then the greater the complexity of the system, as a general rule.

This can be a useful starting point for thinking of writing systems such as academic English as complex. Let's see how.

First, and obviously, writing itself is a system. It is a "group of parts" and "relations between these parts" that enable the system to "function together and form a whole". We can start with the small elements: marks (letters and punctuation) and work upwards through words, phrases, clauses, paragraphs, and more which all function together to make memos for your boss, tweets to your peeps, poems for your lovers, and research papers in your college chemistry class. All of the elements of writing relate in regular ways to other elements, and these relationships form the documents that make writing useful to us humans.

But writing is a system not just within itself but also within other systems — social systems, for instance. Within other systems, writing can act as both one of the elements within the system and as one of the connectors and connections among other elements within the system. Writing connects people — especially texting. Writing is also a part of educational and commercial systems, which I will explore more in future posts.

But is writing a complex system? Yes.

First, writing has lots of elements. I'm not particularly happy with number as a defining parameter of complexity. I think that some systems with few elements (slime mold, for instance) can be complex and some systems with many elements (jet airplanes, for instance) can be merely complicated. Still, by most any measure, writing systems have sufficient number of elements to be considered complex. A study by Google and Harvard estimates over a million words in the history of English, while the Second edition of the Oxford English Dictionary lists about 600,000 words with 171,000 words in current use, and an average of 20,000 to 30,000 words used by individuals. Those are big numbers.

Second, the elements in writing (from letters and punctuation marks to paragraphs) can be connected in countless ways to form an almost infinite number of different documents, most of which feature a surprising degree of novelty. Almost any writer of English can form a sentence that has never before been written yet is still recognizable as English writing. This is astounding.

Third, writing systems can adapt in almost infinite ways to each other and to their environments. We are all witness to the new writings (words, grammars, documents, and more ) that have emerged with modern electronic technology. This blog is itself witness to how a writing system can both map and adapt to new landscapes. Of course, spoken language adapts just as well, but I'm focusing here on writing systems. This means that writing can learn. More on that in later posts.

Finally, writing systems have a sufficient diversity among the elements within the system. In this respect, English writing is somewhat like DNA: it has only 26 letters and a handful of punctuation marks with which to generate countless documents. Though we start with only 26 letters, they can combine and recombine to form countless other elements, just as the four DNA bases can (A, G, C, and T).

So, based on Colchester's brief definition of complex systems, I'm quite comfortable saying that writing systems meet the cut. I'll continue to look at other definitions, but I'm confident that writing will meet those definitions as well. So writing is a complex system. What does that mean? More on that in future posts.

#el30: The Complexity of Data?

Tony873004 [CC BY-SA 4.0
(https://creativecommons.org/licenses/by-sa/4.0)],
from Wikimedia Commons

Stephen Downes frames his E-Learning 3.0 MOOC in Connectivism theory, which claims "that knowledge is essentially the set of connections in a network, and that learning therefore is the process of creating and shaping those networks." As Downes demonstrates later in his course, the connections in a network are composed of nodes and edges. I'm guessing, then, that knowledge--especially the intellectual knowledge that makes up the educational economy--is made up of data (nodes) and the connections (edges) among them that result in some pattern that we call knowledge. Knowledge formation, then, is something like selecting a handful of stars, drawing the connections among them, and calling the resulting network Orion, a name that functions as a hashtag pointing to a body of knowledge about a "giant huntsman whom Zeus placed among the stars as the constellation of Orion" and the various stories about this huntsman and his gods (Wikipedia).

If this is so, then it makes sense that Downes begins his MOOC with a discussion of data, but as I read through his own writing and the suggested readings, I don't find a useful definition of what the MOOC means by data. This becomes a problem for me especially when Downes says that the MOOC addresses "two conceptual challenges: first, the shift in our understanding of content from documents to data; and second, the shift in our understanding of data from centralized to decentralized." This imprecise use of data also disturbs me because shared data and shared arrangements of that data, especially in stories, form the basis for most communities, so for me, data is the key term in his course, but it remains undefined. Perhaps Downes assumes that the concept of data is obvious, but this is exactly the issue for me. Data is not obvious.

Data is complex, and recognizing, selecting, analyzing, and utilizing data is not an exercise in the domain of the simple. Lots of conceptualizing has to happen before we can glibly proceed with any discussion about data or use data as a basis for further discussion. Wikipedia offers a short definition of data that might be useful as a starting point for clarifying some of the issues I have with the concept as used in EL30: data is "a set of values of subjects with respect to qualitative or quantitative variables."

This seems simple enough; however, just a little reconsideration of the definition points us to some immediate problems with data. Data are values, or characteristics, of subjects that we associate with both qualitative and quantitative variables such as scales, numbers, pictures, and words. It doesn't take us long to question if the values or characteristics belong to the object observed, belong to the perceptions of the observer, belong to the notational system employed, or belong to some interactions among the observed, the observer, and the notational system. For instance, does a grade such as an A, one data point, belong to the student graded, the teacher grading, the scale used for grading, or the interactions among all these parts of the system? Traditionally, educators have assumed that grades indicate some characteristic of the student herself. Many of us have come to think that grades indicate just as much about the teachers and testing regimes doing the grading. I think that the single data point emerges rather problematically from the interactions of the student, teacher, testing regime, and the general environment of all.

This is a long and rich conversation that highlights why I'm uncomfortable with the use of data in EL30, and though I will not resolve this issue in this post or even clarify my own developing position, I can say a few things.

I find data to be complex, nontrivial, and problematic for a number of reasons, but first because data is always context dependent. The data that we recognize and the meanings we assign that data depend mostly on the context within which we as observers and the data as the observed are interacting. This immediately puts me in conflict with lots of people who seem to define data as a contextless, and therefore meaningless, collection of points that can be processed into information in some context, as this conversation on ResearchGate suggests. Perhaps this distinction between data and information is useful in certain applications, but it seems ultimately to be misleading.

I don't think we perceive data outside of some context. True, we can change contexts and give data new meaning, but I don't know that we ever perceive data without context, even if our context is confused. For example, consider the period at the end of this sentence --> . That single data point, of course, makes sense only because it is appropriately placed within the context of this blog post, but what if your screen suddenly blinked white out with only the period showing. I think it entirely possible that you might not even see the period, or if you did, you'd think it a faulty pixel, because of course, the frame around your computer screen provides a familiar context for that single data point and you will try to interpret the period within that context. You may not be able to give the period useful meaning--in other words, you may be confused by the single data point--but confusion owes as much to context as does meaning. It's quite possible that perception at all depends upon context.

Wikipedia, "Stars in orion constellation (connected)" 
Attribution-Share Alike 4.0 International

So data is always in some context, and a different context creates different meaning, but data is also dependent on its internal arrangement which is also context dependent. The constellation Orion can be helpful here. As the image to the right shows, Orion looks very much like a graph, a network of data points connected by edges. The stars are the data points, and our imaginations draw the edges to match some story. Of course, we could draw different edges using pretty much the same set of data and match different stories, and in fact, we have done just that in various cultures throughout history. For instance, the ancient Babylonians saw "The True Shepherd of Anu," the ancient Egyptians saw the god Sah, and ancient Indians saw Nataraja, an avatar of Shiva--all by redrawing the connections among the same data points of light. In other words, by changing the arrangement of the data, we get different stories, and by changing the stories, we get different arrangements. Again, the interactions of all the elements yield the meaning of the data, or to say it differently, the meaning of data emerges from the interactions.

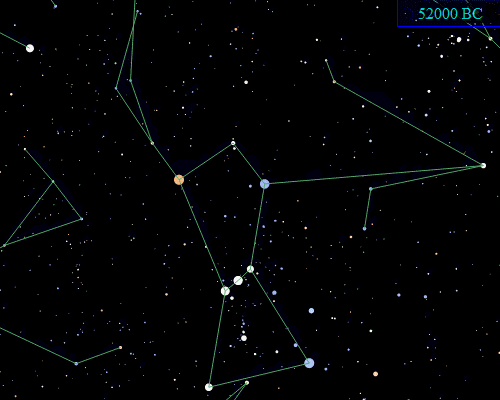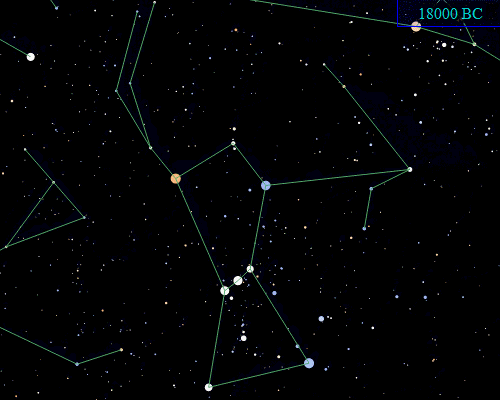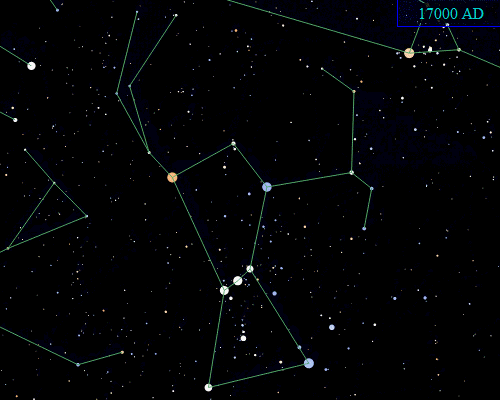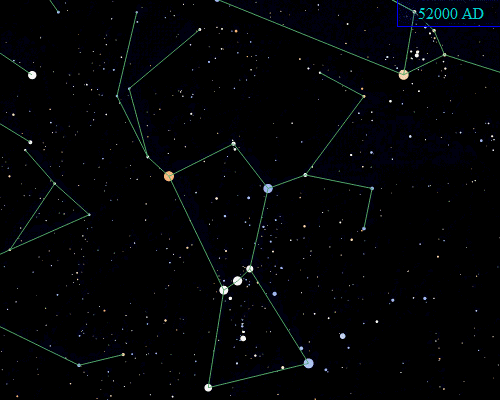
Not only do the edges in a data set, or graph, change, but the data points, or nodes, also shift. We want to think that the stars are immutable--after all, they do not noticeably change during our lifetimes--but our high school science class reminds us that all the seemingly immutable stars are moving at near light speeds across unimaginable distances. The little animation at the top of this post shows the calculated shift of Orion's stars between 40000 BC and 52000 AD. The perceived immutability of the stars is due mostly to the idiosyncratic perception afforded, or I could say imposed, by our position and scale in space/time. During any given lifetime of observing the night sky, the stars seem to stay in place because of the great distances in space/time between us, the observers, and them, the data. If we could readily shift our position and scale in space/time, then we could see quite clearly that our data are moving (the animation above captures a neat shift in scale by compressing 92000 years into a few seconds).



If we do a 3D fly around of Orion—as does this nifty Youtube video—we see that our arrangements of our data are totally owing to our position in space/time relative to the data. If we assume that we are starting at 6:00 o'clock facing the hunter, then by the time we move a quarter-way counterclockwise to 3:00 o'clock, we see something more like a flattened kangaroo, not a hunter or shepherd. And then we remember that Einstein told us a hundred years ago that what we see and measure depends a great deal on our position in space/time relative to the data that we are observing and measuring and that, contrary to our everyday intuition, two different measurements can both be true.

So not only do data points move relative to the observer and to each other, but they also morph within themselves. Data ain't immutable. Consider the data points, the points of light, in Orion: "Betelgeuse … is a massive M-type red supergiant star nearing the end of its life" when it will explode in a supernova about a million years from now—thereby erasing Orion's right shoulder, assuming you think he's facing us rather than facing away. Betelgeuse is also a rogue star, racing through space alone and unattached to any galaxy, unlike the Sun nestled comfortably in the Milky Way. Mintaka, the westernmost star in Orion's belt, is not a single star but "a multiple star system, composed of a large B-type blue giant and a more massive O-type main-sequence star." It looks to the naked eye like a single star only because of its great distance from us. Orion's sword contains the Orion Nebula, not a star at all but a giant nursery for new stars.

Our dataset is breaking down. Rather, our dataset is assuming new arrangements and demonstrably, measurably different values as we change our position in space/time. The old values are not lost, but they are certainly expanded, and at times, supplanted as our relation to and use of the dataset changes. I'm convinced that all data are like this: a collection of characteristics to which we attach certain values depending on the configuration of the artifact and the relative position of the observing node. Let's break this down.

Note first that data is a set of qualitative or quantitative variables associated with an object. Data is always about something else, something real. I draw this assumption from Karl Maton's discussion of ontological realism in his book Knowledge and Knowers: Towards a realist sociology of education (2014). Maton relies on Roy Bhaskar's critical realism when he insists that "knowledge is about something other than itself, that there exists an independently existing reality beyond discourse that helps to shape our knowledge of the world" (10). This is important. As I understand Maton, knowledge is a complex system, or network, of real nodes (real means for Maton entities that possess "properties, powers, and tendencies that have effects" [9] on other entities) that interact with other nodes. Moreover, each node is itself a complex system of other real nodes and their interactions, and each system is a node in enclosing complex systems. The data about any given node emerges from the interactions of all the nodes across all the scales of this system. This understanding is largely consistent, I think, with the Connectivism theory of Downes and Siemens.

Think about a student, Maya, in a classroom. Maya is real in the sense that she has "properties, powers, and tendencies that have effects" upon other students, teachers, books, rooms, heating systems, and so forth. Maya is not, however, just a single node, a single student. She is also a complex system herself comprised one scale down or in of organs, tissues, and interactions among all those nodes. One scale up or out, she is a node within her class, which itself is a node within a school, and so on. All of these nodes across all these scales are real. They all have properties which we can observe and measure both quantitatively and qualitatively and which seduce us into the essentialism of the positivists: that these properties are essential to the entity, that they are, in fact, the entity itself.

Not so, says Maton. The data a teacher collects about a student such as Maya emerges not merely from Maya herself but also from the teacher, from the larger and smaller systems to which both Maya and the teacher belong, and from the knowledge systems of both the teacher and Maya. To my mind, the role of knowledge in complex systems is a key component of Maton's argument. Knowledge becomes a real entity in its own right within whatever system it finds itself. Maton says, "Knowledge practices are both emergent from and irreducible to their contexts of production -- the forms taken by knowledge practice in turn shape those contexts" (11). Just like Maya or her teacher, knowledge has properties, powers, and tendencies that have effects upon other nodes across systems. What is known about Maya affects Maya, her teachers, her classmates, her school, her family, and so on. Of course, effects are reflexive; thus, the knowledge about Maya is in turn affected by the interactions of the other nodes across the systems. Thus, data and knowledge are dynamic and variable, which seduces us into relativism.

But not so fast, says Maton. Knowledge is not merely an individual construct; rather, it emerges from the interactions of all the nodes within a system: the things known, the knowers, and the body of knowledge. Maton is arguing against the epistemological dilemma he finds in much of educational research that is trapped between a positivist essentialism on one hand and a subjectivist relativism on the other. For the hard positivist, qualitative and quantitative data are integral, intimate features of the object itself, unmediated by human intelligence. Red Delicious apples really are red, and all normally functioning humans will see the same red. For the subjective relativist, qualitative and quantitative data are constructs of the observer, fabrications of human intelligence. Red Delicious apples are red because I see them that way in this light, and other humans may see, or construct, different colors based on their culture and personal capacities.

Maton argues for a third way and, to my mind, a more complex way. In his book, he says:

Against positivism, knowledge is understood as inescapably social and historical but, against constructivism, knowledge is not reduced to social power alone, as some knowledge claims have greater explanatory power than others. … Knowledge practices are both emergent from and irreducible to their contexts of production—the forms taken by knowledge practice in turn shape those contexts. … Knowledge is not constructed by individuals as each sees fit but rather produced by actors within social fields of practice characterized by intersubjectively shared assumptions, ways of working, beliefs and so forth. (11)

Knowledge and the data that comprises it are not dependent merely on the objects known or the entities that know, but on both, and on the existing body of knowledge with its notational regimes and on the dynamic interactions within this system. Maton says:

Though knowledge is the product of our minds, it has relative autonomy from knowing—knowledge has emergent properties and powers of its own. This can be seen in the ways knowledge mediates: creativity; learning; and relations among knowers. ... Once formulated as knowledge, 'objectified', our ideas can reshape our knowing. We can both improve and be improved by what we create. (12)

It seems to me then that identifying and using data to form knowledge is not so easy a task as we might think. Though we usually think that data are natural, given, somewhat inert characteristics of the objects under consideration, the case is not so clear. Data associated with any system are complex, emergent properties of the interactions within the system, interactions among the system observed, the system observing, and other systems at the same scale, and finally the interactions among the observed system and the enclosing systems. Nothing about this is trivial, or simple, and the complexity of data holds great significance for any discussion of data.

First, the idea that the observer is an integral node in whatever system is being observed is one of the great insights of Twentieth-century science and a necessary corrective of classical science's assumption of objectivity—that scientists can stand apart from their experiments and observe and report without affecting the observed system. Complexity science says that observers are an integral, functioning part of the system being observed and that their relative position in space/time must always be accounted for. In short, observations depend on what both the observed and the observer bring to the observation.

This does not mean, however, as Maton has argued to my satisfaction, that data depend solely on either the mental constructs of the observer or the objective characteristics of the observed. The object observed does really exist in its own right and brings its own agency, powers, and presence to bear on any observation or measurement of it. The data observed, collected, and analyzed about the student Maya depend as much on Maya herself as on the teachers and schools collecting the data. More properly stated, the data emerge from the relative positions and interactions between Maya and her teachers.

But this is not the whole story. Observed and observers alike exist and interact within systems of knowledge that can be complementary and consistent or contradictory and conflicting. These stories, paradigms, and belief systems affect what the observed can reveal about itself and what the observer can see, or know. What Maya reveals about herself to teachers and schools and what the teachers and schools can see of Maya depends not just on Maya and the teachers and their interactions but also on the stories, paradigms, and belief systems that each brings to the observation.

Maton is quite clear about the reality and agency of a system of knowledge when he says:

We do not learn about the world in an unmediated and direct fashion but rather in relation to existing and objectified knowledge about the world. We can 'plug into' existing knowledge and so do not have to start from scratch or attempt by ourselves to recreate what has taken, in the case of 'academic' knowledge, thousands of years and even more minds to develop.

What data teachers can recognize and collect about Maya depends a great deal on the system of knowledge, the paradigms and belief systems, out of which they function. I think EL30 would have benefited from some discussion of data prior to using it so extensively in the class.

Though it now occurs to me that Downes might have assumed that Connectivism provides an adequate context for his use of data. If that's the case, then he could have easily mentioned it, but then I might not have taken the opportunity to look more carefully into it myself.